19.质数

发表于 分类于 ， 本文字数： 2k

质数

若一个数，只有一和它本身两个因子，那么这个数就是一个质数

在自然数集中，小于n的质数约有ln(n)个

质数的判定

###试除法

试除法是常用的判断素数的方法
时间复杂度O ( n^1/2^ ) 

1
2
3
4
5
6
7
8
inline bool is_prime(int x){
    if(x < 2)
        return false;
    for(register int i = 2;i*i <= x ++i)
        if(x % i == 0)
            return false;
    return true;
}

Miller-Robbin算法

根据人品判断质数（雾 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
int modexp(int a,int b,int m)
{
    __int64 ans=1;__int64 t=a%m;
    while(b)
    {
        if(b&1)
        {
            ans=(ans*t)%m;
            b--;
        }
        t=(t*t)%m;
        b>>=1;
    }
    return ans;
}

bool MillerRobbin(int n)
{
    if(n==2) return 1;
    else if((n&1)==0) return 0;
    int a,d;
    long long t;
    for(int i=0;i<s;i++)
    {
        a=rand()%(n-1)+1;
        d=n-1;
        while((d&1)==0) d>>=1;
        t=modexp(a,d,n);
        while(d!=n-1&&t!=1&&t!=n-1)
        {
            t=(t*t)% n;
            d<<=1;
        }
        if(t==n-1||(d&1)==1) continue;
        else return 0;
    }
    return 1;
}

浅谈 Miller-Robbin 与 Pollard Rho

质数的筛选

Eratosthenes筛选（埃拉托色尼筛法）

每次只用素数去筛复杂度O(nloglogn)

1
2
3
4
5
6
7
8
9
10
11
int v[N];
void primes(int n{
    memset(v,0,sizeof v);
    for(int i = 2;i <= n; ++i){
        if( v[i] )continue;
        cout<<i<<endl;
        for(int j = i;j <= n/i;++j)
            v[i*j] = 1;
    }
}

线型筛（欧拉筛）

每次只用一个数用小于当前这个数最小质因子的质数去筛其他数，即保证每个数都被自己的最小质因子筛掉。O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
const int N = 10005;
int n,prime[N],cnt;
bool vis[N];

inline void primes()
{
	for(register int i = 2;i <= n;i ++)
    {
    	if(!vis[i]) prime[++cnt] = i;
    	for(register int j = 1;j <= cnt && i * prime[j] <= n; j ++)
        {
        	vis[i * prime[j]] = 1;
            if(i % prime[j] == 0) break;
    	}
    }
}

质因数分解

任何一个大于1的数都可以被分解成有限个质数乘积的形式

试除法

1
2
3
4
5
6
7
8
9
10
11
12
const int N = 1005;
int p[N];
inline int factorize(int x)
{
	register int cnt = 0;
	for(register int i = 2;i * i <= x;i ++)
		while(x % i == 0)
			p[++cnt] = i, x /= i;	
	if(x > 1) p[++cnt] = x;
	return cnt;
}

更优的写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/* 有点二进制拆分的意思 */
vector<int>p;//存质数
vector<int>factor(int n){
    vector<int>f;
    for(int i = 0;i < p.size();++i){
        if(p[i]*p[i] > n)
            break;
        while(n % p[i] == 0)//直接从质数里挑
            f.push_back(p[i]),n /= p[i]; 
    }
    if(n>1)//如果还有
        f.push_back(n);
    return f;
}

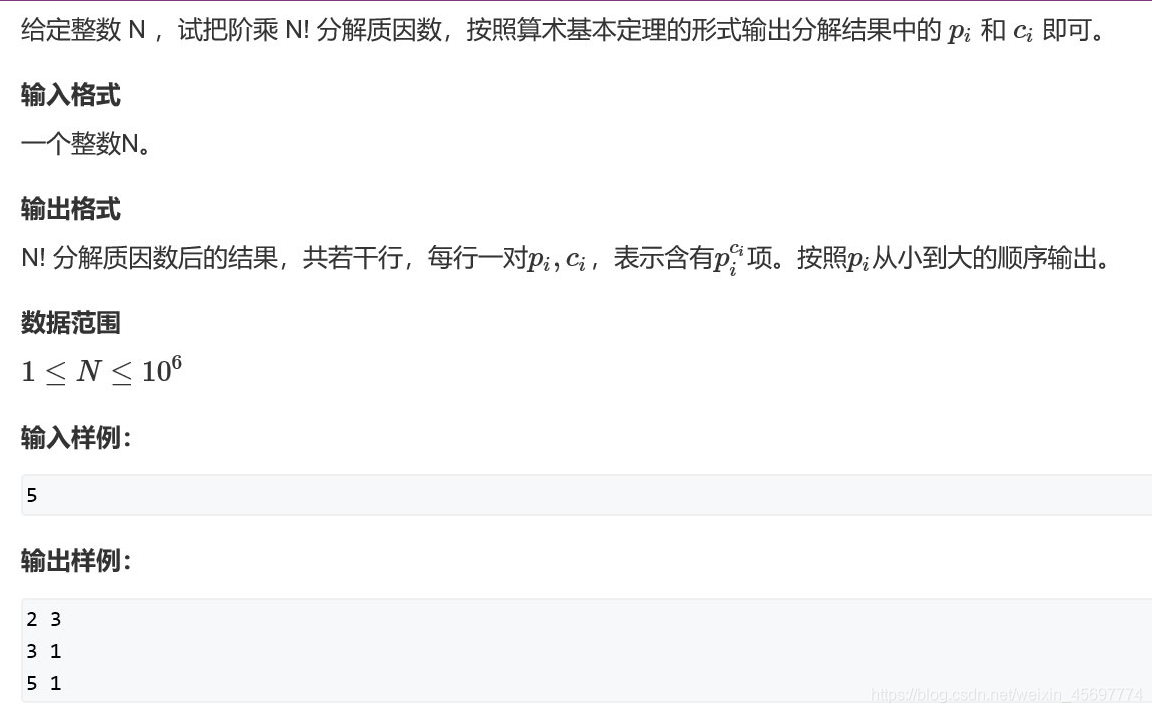
在这里插入图片描述

样例解释
5 ! = 120 = 2^3^35
N!中质数因子p的个数,就是1~N中每个数中含有的质因数p的个数.既然如此的话,那么我们发现,1～N中，p的倍数，至少有一个质因子p的显然有 n/p

个,而至少有两个质因子p数的显然是有 n/p^2^ ，以此类推。

------ 本文结束感谢您的阅读 ------
请我一杯咖啡吧！
itingyu 微信打赏 微信打赏