8.数据结构优化dp

发表于 分类于 ， 本文字数： 4.4k

在DP的转移中需要用到某一个阶段的最值的时候可以用线段树和树状数组等数据结构进行维护，在O(1)或O(log N) 的时间复杂度内完成转移

https://www.luogu.com.cn/problem/P4644

[USACO05DEC] Cleaning Shifts S

题目描述

约翰的奶牛们从小娇生惯养，她们无法容忍牛棚里的任何脏东西。约翰发现，如果要使这群有洁癖的奶牛满意，他不得不雇佣她们中的一些来清扫牛棚，约翰的奶牛中有 $ N(1 \leq N \leq 10000) $ 头愿意通过清扫牛棚来挣一些零花钱。

由于在某个时段中奶牛们会在牛棚里随时随地地乱扔垃圾，自然地，她们要求在这段时间里，无论什么时候至少要有一头奶牛正在打扫。需要打扫的时段从某一天的第 $ M $ 秒开始，到第 $ E $ 秒结束 $ (0 \leq M \leq E \leq 86399) $。注意这里的秒是指时间段而不是时间点，也就是说，每天需要打扫的总时间是 $ E-M+1 $ 秒。

约翰已经从每头牛那里得到了她们愿意接受的工作计划：对于某一头牛，她每天都愿意在笫 $ T_1 \ldots T_2 $ 秒的时间段内工作 $ (M \leq T_1 \leq T_2 \leq E) $ ，所要求的报酬是 $ S $ 美元 $ (0 \leq S \leq 500000) $。与需打扫时段的描述一样，如果一头奶牛愿意工作的时段是每天的第 $ 10 \ldots 20 $ 秒，那她总共工作的时间是 $ 11 $ 秒，而不是 $ 10 $ 秒。

约翰一旦决定雇佣某一头奶牛，就必须付给她全额的工资，而不能只让她工作一段时间，然后再按这段时间在她愿意工作的总时间中所占的百分比来决定她的工资。现在请你帮约翰决定该雇佣哪些奶牛以保持牛棚的清洁，当然，在能让奶牛们满意的前提下，约翰希望使总花费尽量小。

输入格式

第 $ 1 $ 行： $ 3 $ 个正整数 $ N,M,E $ 。

第 $ 2 $ 到 $ N+1 $ 行：第 $ i+1 $ 行给出了编号为 $ i $ 的奶牛的工作计划，即 $ 3 $ 个正整数 $ T_1,T_2,S $ 。

输出格式

输出一个整数，表示约翰需要为牛棚清理工作支付的最少费用。如果清理工作不可能完成，那么输出 $ -1 $ 。

样例 #1

样例输入 #1

1
2
3
4
3 0 4
0 2 3
3 4 2
0 0 1

样例输出 #1

1
5

提示

约翰有 $ 3 $ 头牛，牛棚在第 $ 0 $ 秒到第 $ 4 $ 秒之间需要打扫。 约翰雇佣前两头牛清扫牛棚，可以只花 $ 5 $ 美元就完成一整天的清扫。

首先设计出状态，dp[x]表示从m清理到x所付出的最小代价
很显然，状态转移方程为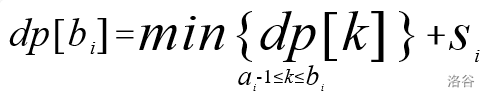
img
很显然，我们的每一次的转移都会用到一个区间的最小值，所以考虑运用线段树进行优化

build

我们在[m,e]上建立一颗线段树，存储DP的最小值

change

当我们更新完一个DP的值的时候，就在线段树中插入这个值

ask

每一次状态转移我们都需要在区间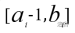img查找最小值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#include<bits/stdc++.h>
using namespace std;

const int MAXN=1e5+5,MAXM=9e5+5;
struct Node
{
	int t1,t2,s;
}cow[MAXN];
struct node
{
	int l,r,val;
}lst[MAXM];
int n,s,e,dp[MAXM],ans;

void build_tree(int id,int l,int r)
{
	lst[id].l=l; lst[id].r=r;
	if( l==r )
	{
		lst[id].val=dp[l];
		return;
	}
	
	int mid=(l+r)/2;
	build_tree(id*2,l,mid);
	build_tree(id*2+1,mid+1,r);
	lst[id].val=min(lst[id*2].val,lst[id*2+1].val);
	return;
}

void change_tree(int id,int ver,int val)
{
	if( lst[id].l==lst[id].r )
	{
		lst[id].val=dp[ver];
		return;
	}
	
	int mid=(lst[id].l+lst[id].r)/2;
	if( mid >= ver ) change_tree(id*2,ver,val);
	else change_tree(id*2+1,ver,val);
	lst[id].val=min(lst[id*2].val,lst[id*2+1].val);
	return;
}

int ask_tree(int id,int l,int r)
{
	if( lst[id].l==lst[id].r ) return lst[id].val;
	
	int mid=(lst[id].l+lst[id].r)/2,tem=0x7f7f7f7f;
	if( mid >= l ) tem=min(tem,ask_tree(id*2,l,r));
	if( mid <= r ) tem=min(tem,ask_tree(id*2+1,l,r));
	return tem;
}

bool cmp(Node x,Node y)
{
	return x.t2 < y.t2;
}

int main()
{
	scanf("%d%d%d",&n,&s,&e);
	for(int i=1;i<=n;i++) scanf("%d%d%d",&cow[i].t1,&cow[i].t2,&cow[i].s);
	sort(cow+1,cow+n+1,cmp);
	memset(dp,0x7f7f7f7f,sizeof(dp));
	dp[s]=0;
	build_tree(1,s,e);
	for(int i=1;i<=n;i++)
	{
		int tem=ask_tree(1,cow[i].t1-1,cow[i].t2);
		dp[cow[i].t2]=tem+cow[i].s;
		if( cow[i].t2 >= e ) {ans=dp[cow[i].t2]; break;}
		change_tree(1,cow[i].t2,dp[i]);
	}
	if( ans==2139075787 ) printf("-1");
	else printf("%d",ans);
	return 0;
}

The Battle of Chibi

题面翻译

$T$ 组数据，在长度为 $n$ 的数列 $a$ 中，求出长度为 $m$ 的严格上升子序列的个数。答案对 $10^9 + 7$ 取模。

举个例子：

$n = 5$，$m = 3$，$a$ 为 1 3 2 4 5。

那么符合条件的序列就有：1 3 4，1 2 5，1 3 5，1 4 5，3 4 5。最终答案就是 $5$。

数据范围：

$1 \le m \le n \le 1000$，$1 \le a_i \le 10^9$，$1 \le T \le 100$。

题目描述

PDF

输入格式

输出格式

样例 #1

样例输入 #1

1
2
3
4
5
2
3 2
1 2 3
3 2
3 2 1

样例输出 #1

1
2
Case #1: 3
Case #2: 0
分析

实际上是给定一个长度为N的数列，求数列中有多少个长度为M的严格递增子序列
首先设计状态 dp[i] [j] 表示前j个数中以第j个数为结尾的长度为i 的严格递增序列有多少个

状态转移方程为：

img

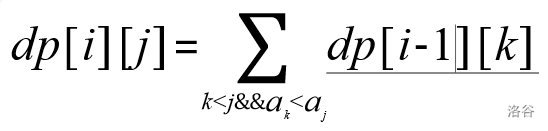
add

将c[disc[j]]增加dp[i-1] [j]

ask

查询disc[j]的前缀和

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include<bits/stdc++.h>
using namespace std;

const int MAXN=1e3+5,mod=1e9+7;
struct Node
{
	int id,val;
}a[MAXN],b[MAXN];
int c[MAXN],disc[MAXN],n,m,t,dp[MAXN][MAXN];

int lowbit(int x)
{
	return x & -x;
}

bool cmp(Node x,Node y)
{
	return x.val == y.val ? x.id > y.id : x.val < y.val;
}

int ask(int x)
{
	int tem=0;
	while( x )
	{
		tem+=c[x]; tem%=mod;
		x-=lowbit(x);
	}
	return tem;
}

void add(int x,int y)
{
	while( x <= n+1 )
	{
		c[x]+=y; c[x]%=mod;
		x+=lowbit(x);
	}
	return;
}

void work(int k)
{
	memset(a,0,sizeof(a)); memset(dp,0,sizeof(dp));
	memset(disc,0,sizeof(disc));
	dp[0][0]=1;
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) scanf("%d",&a[i].val),a[i].id=i,b[i]=a[i];
	sort(b+1,b+n+1,cmp);
	for(int i=1;i<=n;i++) disc[b[i].id]=i+1;
	for(int i=1;i<=m;i++)
	{
		memset(c,0,sizeof(c));
		add(1,dp[i-1][0]);
		for(int j=1;j<=n;j++)
		{
			dp[i][j]=ask(disc[j]-1);
			add(disc[j],dp[i-1][j]);
		}
	}
	int ans=0;
	for(int i=1;i<=n;i++) ans+=dp[m][i],ans%=mod;
	printf("Case #%d: %d\n",k,ans%mod);
	return;
}

int main()
{
	scanf("%d",&t);
	for(int i=1;i<=t;i++) work(i);
	return 0;
}
------ 本文结束感谢您的阅读 ------
请我一杯咖啡吧！
itingyu 微信打赏 微信打赏