16.树与图的遍历

发表于 分类于 ， 本文字数： 4.5k

深度优先遍历

深度优先遍历，就是在每个点x上面的的多条分支时，任意选择一条边走下去，执行递归，直到回溯到点x后再走其他的边 

1
2
3
4
5
6
7
8
9
10
11
12
int vis[N];//标记每一个点的状态

void dfs(int u){
    vis[u] = 1;
    for(int i = head[u];i;i = nex[i]){
        int v = ver[i];
        if(vis[v])
            continue;
        dfs(v);
    }
}

时间戳

按照上述的深度优先遍历的过程，以每一个结点第一次被访问的顺序，依次赋值1~N的整数标记，该标记就被称为时间戳。
标记了每一个结点的访问顺序。

树的DFS序(树链剖分前驱知识)

一般来说，我们在对树的进行深度优先时，对于每个节点，在刚进入递归时和回溯前各记录一次该点的编号，最后会产生一个长度为2N的序列，就成为该树的DFS序。

1
2
3
4
5
6
7
8
9
10
11
12
int a[N],cnt;
int dfs(int u){
     a[++cnt] = u;//用a数组存DFS序
     vis[u] = 1;
     for(int i = head[u]; i;i = nex[i]){
        int v = ver[i];
        if(vis[v])
            continue;
        dfs(v);
     }
     a[++cnt] = u;
}

1688142098509

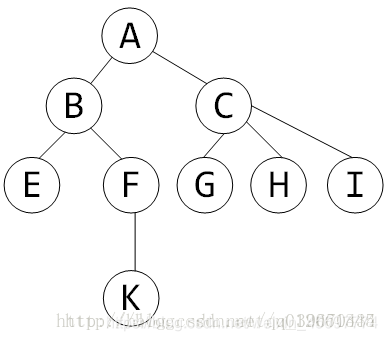
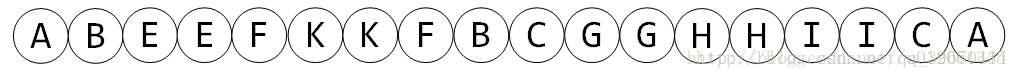
在这里插入图片描述

在这里插入图片描述

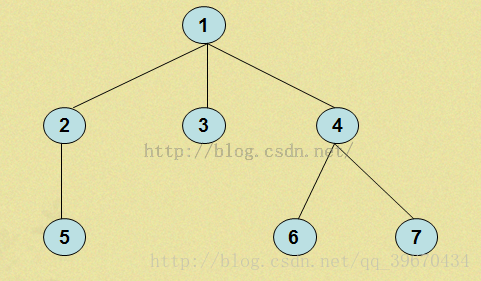
这里写图片描述

如下图，DFS之后，那么树的每个节点就具有了区间的性质。

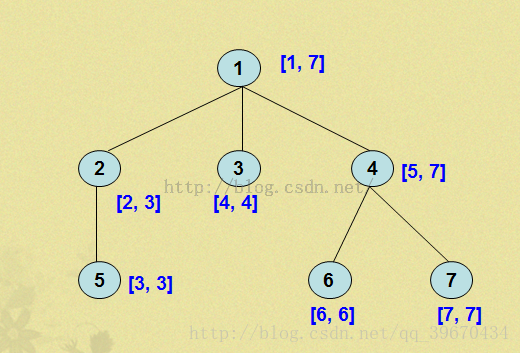
这里写图片描述

dfs序的七个基本问题：

ps:deep[x]为x的深度，l[x]为dfs序中x的位置，r[x]为dfs序中x子树的结束位置

1.点修改，子树和查询

　　在dfs序中，子树处于一个连续区间中。所以这题可以转化为：点修改，区间查询。用树状数组或线段树即可。

2.树链修改，单点查询

　　将一条树链x,y上的所有点的权值加v。这个问题可以等价为：

　　1）.x到根节点的链上所有节点权值加v。

　　2）.y到根节点的链上所有节点权值加v。

　　3）.lca（x,y）到根节点的链上所有节点权值和减v。

　　4）.fa(lca(x,y))到根节点的链上所有节点权值和减v。　　

　　上面四个操作可以归结为：节点x到根节点链上所有节点的权值加减v。修改节点x权值，当且仅当y是x的祖先节点时，x对y的值有贡献。

　　所以节点y的权值可以转化为节点y的子树节点贡献和。从贡献和的角度想：这就是点修改，区间和查询问题。

　　修改树链x,y等价于add(l[x],v),add(l[y],v),add(l[lca(x,y)],-v),add(l[fa(lca(x,y))],-v)。

　　查询：get_sum(r[x])-get_sum(l[x]-1)

　　用树状数组或线段树即可。

3.树链修改，子树和查询

　　树链修改部分同上一问题。下面考虑子树和查询问题：前一问是从贡献的角度想，子树和同理。

　　对于节点y其到根节点的权值和，考虑其子节点x的贡献：w[x](deep[x]-deep[y]+1) = w[x](deep[x]+1)-w[x]*deep[y]

　　所以节点y的子树和为：

　　

　　ps:公式中的v[i]为手误，应为w[i]。

　　所以用两个树状数组或线段树即可：

　　　　第一个维护∑w[i]*(deep[i]+1):支持操作单点修改，区间和查询。（这也就是问题2）

　　　　第二个维护∑ w[i]：支持操作单点修改，区间查询。（这其实也是问题2）

4.单点更新，树链和查询

　　树链和查询与树链修改类似，树链和(x,y)等于下面四个部分和相加：

　　1）.x到根节点的链上所有节点权值加。

　　2）.y到根节点的链上所有节点权值加。

　　3）.lca（x,y）到根节点的链上所有节点权值和的-1倍。

　　4）.fa(lca(x,y))到根节点的链上所有节点权值和的-1倍。

　　所以问题转化为：查询点x到根节点的链上的所有节点权值和。

　　修改节点x权值，当且仅当y是x的子孙节点时，x对y的值有贡献。

　　差分前缀和，y的权值等于dfs中[1,l[y]]的区间和。

　　单点修改：add(l[x],v),add(r[x]+1,-v);

5.子树修改，单点查询

　　修改节点x的子树权值，在dfs序上就是区间修改，单点权值查询就是单点查询。

　　区间修改，单点查询问题：树状数组或线段树即可;

6.子树修改，子树和查询

　　题目等价与区间修改，区间查询问题。用树状数组或线段树即可。

7.子树修改，树链查询

　　树链查询同上，等价为根节点到y节点的链上所有节点和问题。

　　修改节点x的子树权值，当且仅当y是x的子孙节点时（或y等于x），x对y的值有贡献。

　　x对根节点到y节点的链上所有节点和的贡献为：w[x]*(deep[y]-deep[x]+1)=w[x]deep[y]-w[x](1-deep[x])

　　同问题三，用两个树状数组或线段树即可。

树的深度

树中各个节点的深度是一种自顶向下的统计信息

起初，我们已知根节点深度是0.若节点x的深度为d[x],则它的子结点 y yy 的深度就是d[y]=d[x]+1

1
2
3
4
5
6
7
8
9
10
11
12
int dep[N];
void dfs(int u){
	vis[u] = 1;
	for(int i = head[u];i;i = nex[i]){
		int v = ver[i];
		if(vis[v])
			continue;
		dep[v] = dep[u]+1;//父结点 u 到子结点 v  递推 
		dfs(v);
	}
}

树的重心与size

树的重心是自底向上统计的
树的重心也叫树的质心。对于一棵树n个节点的无根树，找到一个点，使得把树变成以该点为根的有根树时，最大子树的结点数最小。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

int vis[N];
int Size[N];
int ans = INF;
int id;
void dfs(int u){
    vis[u] = 1;
    Size[u] = 1;//子树的大小
    int max_part = 0;
    for(int i = head[u];i;i = nex[i]){
        int v = ver[i];
        if(vis[v])
            continue;
        dfs(v);
        Size[u] += Size[v];
        max_part = max(max_part,Size[v]);//比较儿子的size因为这里是假设以u为重心
    }
    max_part = max(max_part,n-Size[u]);//n为整棵树的结点数
    if(max_part<ans){//更新
        ans = max_part;//记录重心对应的max_part的值
        id = u;//记录重心位置
    }
}

图的连通块划分

若在一个无向图中的一个子图中任意两个点之间都存在一条路径（可以相互到达），并且这个子图是“极大的”（不能在扩展），则称该子图是原图的一个联通块

如下代码所示，cnt是联通块的个数，v记录的是每一个点属于哪一个联通块
经过连通块划分，可以将森林划分出每一颗树，或者将图划分为各个连通块。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int cnt;
void dfs(int u){
    vis[u] = cnt;//这里存的是第几颗树或者是第几块连通图
    for(int i = head[u];i;i = nex[i]){
        int v = ver[i];
        if(vis[v])
            continue;
        dfs(v);
    }
}
int main()
{
    for(int i = 1;i<=n;++i){
        if(!vis[i])//如果是颗新树就往里面搜
            ++cnt,dfs(i);
    }
}

广度优先搜索

树与图的广度优先遍历，顺便求d数组（树结点的深度/图结点的层次）。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void bfs(){
    memset(d,0,sizeof d);
    queue<int>q;
    q.push(1);
    d[1] = 1;
    while(q.size()){
        int u = q.front();
        q.pop();
        for(int i = head[u];i;i = nex[i]){
            int v = ver[i];
            if(d[v])continue;
            d[v] = d[u]+1;
            q.push(v);
        }
    }
}

广度优先遍历是一种按照层次顺序访问的方法。
它具有两个重要的性质：

  1. 在访问完所有的第i层结点后，才会访问第i+1层结点。
  2. 任意时刻，队列中只会有两个层次的结点，满足“两段性”和“单调性”。

拓扑排序

给定一张有向无环图，若一个序列A满足图中的任意一条边(x,y)x都在y的前面呢么序列A就是图的拓扑排序

求拓扑序的过程非常简单我们只需要不断将入度为0的点加入序列中即可
（入度：有向图中以结点x为终点的有向边的条数）
（出度：有向图中以结点x为起点的有向边的条数）
（无向图中的度：以x为端点的无向边的条数）

1.建立空拓扑序列A
2.预处理出所有入度为deg[i],起初把入度为0的点入队
3.取出队列头节点x,并把x放入队列A中
4.对于从x出发的每条边(x,y)，把deg[y]减1，若deg[y] = 0 ,把y加入队列中
5.重复3，4直到队列为空，此时A即为所求

拓扑排序可以判定有向图中是否存在环。若拓扑排序以后的A序列的长度小于图中点的长度，说明有的点没有被遍历，进而说明存在环。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
int head[N],ver[N],nex[N],edge[N],tot;
int n,m;
int deg[N];
int A[N];
void add(int u,int v){
    ver[++tot] = v;
    nex[tot] = head[u];
    head[u] = tot;
    deg[v]++;//入度加1
}
int cnt;
void toposort(){//拓扑排序
    queue<int>q;
    for(int i = 1;i<=n;++i)
        if(deg[i] == 0)q.push(i);//步骤2，先找所有度为0的点
    while(q.size()){
        int u = q.front();
        q.pop();
        A[++cnt] = u;
        for(int i = head[u];i;i = nex[i]){
            int v = ver[i];
            if(--deg[v] == 0)
                q.push(v);
        }
    }
}
int main()
{
    cin>>n>>m;
    for(int i = 1;i <=m;++i){
        int x,y;
        scanf("%d%d",&x,&y);
        add(x,y);
    }
    toposort();
    for(int i = 1;i <=cnt;++i){
        printf("%d ",A[i]);
    }
    puts("");
    return 0;
}
------ 本文结束感谢您的阅读 ------
请我一杯咖啡吧！
itingyu 微信打赏 微信打赏