2.平衡二叉树(AVL)

为了保证不退化成线性查找，就要维持树的平衡。这个平衡条件要容易保持，从而保证树的深度为O(logN)，很容易想到两种平衡条件：

1. 最简单的是要求左右子树具有相同的高度。
2. 另一种是要求每个节点都必须有相同高度的左子树和右子树。

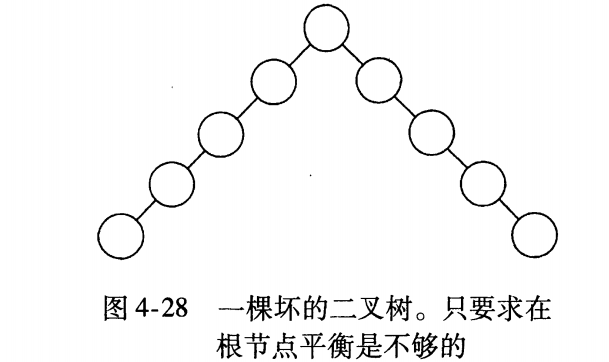
然而，这两种要求都太严格而难以使用。

1.AVL树(Adelson-Velskii 和 Laandis)

AVL树得名于它的发明者 G.M. Adelson-Velsky 和 E.M. Landis，是最早被发明的一种平衡树。平衡二叉树本质上还是一颗二叉查找树，只是带上了平衡条件。

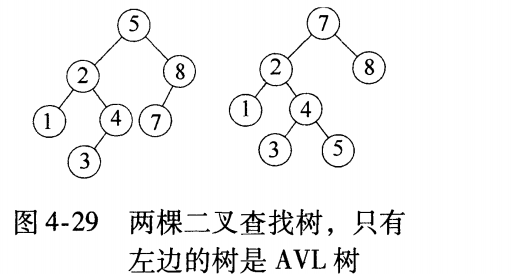
一棵平衡二叉树是每个节点的左子树和右子树的高度最多差1的二叉查找树。

• 平衡二叉树是带有平衡条件的二叉查找树
• 平衡二叉树的每个节点的左子树和右子树的高度最多差1

1.1AVL树的特点

AVL树中的每个节点的左子树和右子树的高度差不会大于1。在插入时，检查新节点的插入点所在的最低子树的根。如果它的子节点的高度相差大于1，则会破坏原有的平衡性，因此需要进行旋转操作以达到再次平衡，此时会执行一次或两次旋转使他们的高度相等。然后算法向上移动，检查上面的节点，必要时均衡高度。这个检测检查所有路径一直向上，直到根为止。

1.2.AVL树的缺点

由于插入(或删除)一个节点时需要扫描两趟树，一次向下查找插入点，一次向上平衡树，所以AVL树不如下面介绍的红黑树效率高，也不如红黑树常用。

(也就是说为了保持平衡，平衡二叉树定义节点的左子树和右子树的高度差不大于1，这种规定过于严格，导致在做插入或删除操作时需要自底向上逐层检查节点的平衡性(高度差)，因此效率较低)

请我一杯咖啡吧！

赞赏

微信打赏