堆排序

发表于 2023-07-01 分类于数据结构与算法，排序算法，选择排序本文字数： 3.5k

堆一般指的是二叉堆，顾名思义，二叉堆是完全二叉树或者近似完全二叉树

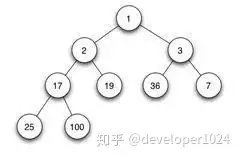
堆

1. 堆的性质

① 是一棵完全二叉树
② 每个节点的值都大于或等于其子节点的值，为最大堆；反之为最小堆。

2. 堆的存储

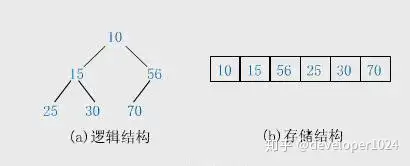
一般用数组来表示堆，下标为 i 的结点的父结点下标为(i-1)/2；其左右子结点分别为 (2i + 1)、(2i + 2)

3. 堆的操作

在堆的数据结构中，堆中的最大值总是位于根节点(在优先队列中使用堆的话堆中的最小值位于根节点)。堆中定义以下几种操作：

① 最大堆调整（Max_Heapify）：将堆的末端子节点作调整，使得子节点永远小于父节点
② 创建最大堆（Build_Max_Heap）：将堆所有数据重新排序
③ 堆排序（HeapSort）：移除位在第一个数据的根节点，并做最大堆调整的递归运算

##堆排序（Heap Sort）

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

1. 基本思想

利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性，使得每次从无序中选择最大记录(最小记录)变得简单。

① 将待排序的序列构造成一个最大堆，此时序列的最大值为根节点
② 依次将根节点与待排序序列的最后一个元素交换
③ 再维护从根节点到该元素的前一个节点为最大堆，如此往复，最终得到一个递增序列

2. 实现逻辑

① 先将初始的R[0…n-1]建立成最大堆，此时是无序堆，而堆顶是最大元素。
② 再将堆顶R[0]和无序区的最后一个记录R[n-1]交换，由此得到新的无序区R[0…n-2]和有序区R[n-1]，且满足R[0…n-2].keys ≤ R[n-1].key
③ 由于交换后新的根R[1]可能违反堆性质，故应将当前无序区R[1..n-1]调整为堆。然后再次将R[1..n-1]中关键字最大的记录R[1]和该区间的最后一个记录R[n-1]交换，由此得到新的无序区R[1..n-2]和有序区R[n-1..n]，且仍满足关系R[1..n-2].keys≤R[n-1..n].keys，同样要将R[1..n-2]调整为堆。
④ 直到无序区只有一个元素为止。

3. 动图演示

堆排序算法的演示。首先，将元素进行重排，以匹配堆的条件。图中排序过程之前简单的绘出了堆树的结构。

分步解析说明：

实现堆排序需要解决两个问题：

1、如何由一个无序序列建成一个堆？
2、如何在输出堆顶元素之后，调整剩余元素成为一个新的堆？

假设给定一个组无序数列{100,5,3,11,6,8,7}，带着问题，我们对其进行堆排序操作进行分步操作说明。

3.1 创建最大堆

①首先我们将数组我们将数组从上至下按顺序排列，转换成二叉树：一个无序堆。每一个三角关系都是一个堆，上面是父节点，下面两个分叉是子节点，两个子节点俗称左孩子、右孩子；

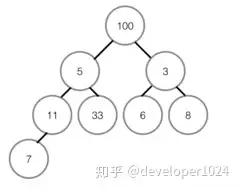
②转换成无序堆之后，我们要努力让这个无序堆变成最大堆(或是最小堆)，即每个堆里都实现父节点的值都大于任何一个子节点的值。

③从最后一个堆开始，即左下角那个没有右孩子的那个堆开始；首先对比左右孩子，由于这个堆没有右孩子，所以只能用左孩子，左孩子的值比父节点的值小所以不需要交换。如果发生交换，要检测子节点是否为其他堆的父节点，如果是，递归进行同样的操作。

④第二次对比红色三角形内的堆，取较大的子节点，右孩子8胜出，和父节点比较，右孩子8大于父节点3，升级做父节点，与3交换位置，3的位置没有子节点，这个堆建成最大堆。

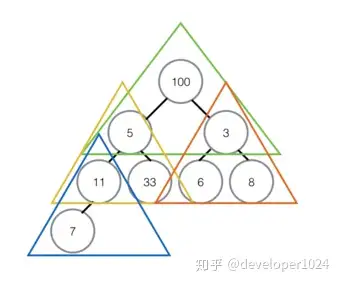
⑤对黄色三角形内堆进行排序，过程和上面一样，最终是右孩子33升为父节点，被交换的右孩子下面也没有子节点，所以直接结束对比。

⑥最顶部绿色的堆，堆顶100比左右孩子都大，所以不用交换，至此最大堆创建完成。

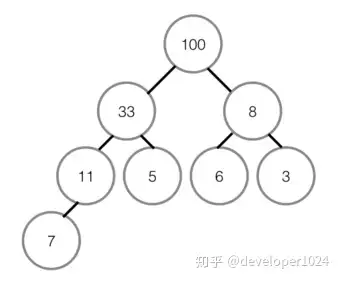
3.2 堆排序（最大堆调整）

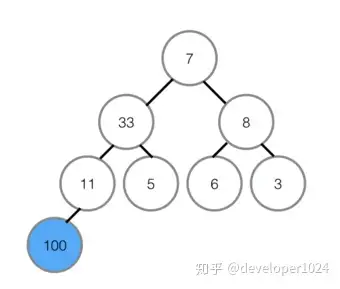
①首先将堆顶元素100交换至最底部7的位置，7升至堆顶，100所在的底部位置即为有序区，有序区不参与之后的任何对比。

②在7升至顶部之后，对顶部重新做最大堆调整，左孩子33代替7的位置。

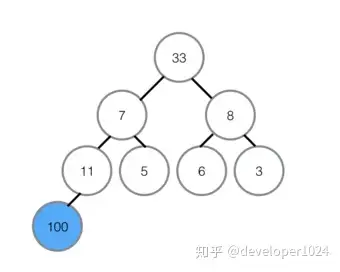
③在7被交换下来后，下面还有子节点，所以需要继续与子节点对比，左孩子11比7大，所以11与7交换位置，交换位置后7下面为有序区，不参与对比，所以本轮结束，无序区再次形成一个最大堆。

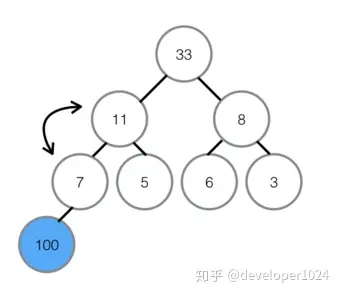
④将最大堆堆顶33交换至堆末尾，扩大有序区；

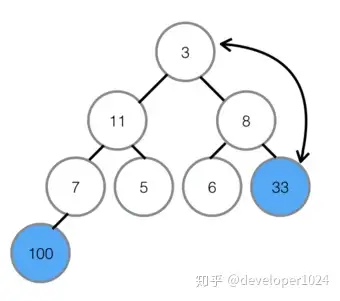
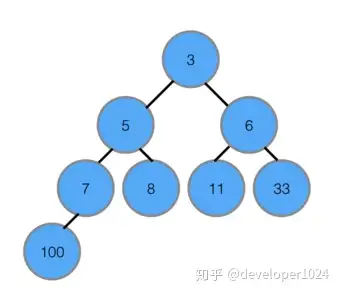
⑤不断建立最大堆，并且扩大有序区，最终全部有序。

4. 复杂度分析

平均时间复杂度：O(nlogn)
最佳时间复杂度：O(nlogn)
最差时间复杂度：O(nlogn)
稳定性：不稳定

堆排序其实也是一种选择排序，是一种树形选择排序。只不过直接选择排序中，为了从R[1…n]中选择最大记录，需比较n-1次，然后从R[1…n-2]中选择最大记录需比较n-2次。事实上这n-2次比较中有很多已经在前面的n-1次比较中已经做过，而树形选择排序恰好利用树形的特点保存了部分前面的比较结果，因此可以减少比较次数。对于n个关键字序列，最坏情况下每个节点需比较log2(n)次，因此其最坏情况下时间复杂度为nlogn。堆排序为不稳定排序，不适合记录较少的排序。

代码实现

public class HeapSort {

    int data[];

    public HeapSort(int[] data){
        this.data = data;
    }
     private void sink(int index,int len){
        int child = (index<<1)+1;
        if(child>len-1){
            return;
        }else {
            if(child+1<len&&(data[child]<data[child+1])){
                child++;
            }
            if(data[index]>=data[child]){
                return;
            }
            swap(index,child);
            sink(child,len);
        }
    }
    public void sort(){
      //可以用raise按顺序添加，建立大顶堆
//        for (int i = 0; i < data.length ; i++) {  
//            raise(i);
//        }
//        System.out.println(Arrays.toString(data));
        // 用下面倒序调整，建立大顶堆
        for (int i = data.length/2; i >=0; i--) { 
            sink(i,data.length);
        }
        for (int i = data.length-1; i >0; i--) {
            System.out.println(Arrays.toString(data));
            swap(0,i);
            sink(0,i);
        }
    }

    private void swap(int i,int j){
        data[i]^=data[j];
        data[j]^=data[i];
        data[i]^=data[j];
    }
    private void raise(int index){
        if(index==0){
            return;
        }
        if(data[(index-1)/2]>=data[index]) {
            return;
        }
        swap(index,(index-1)/2);
        raise((index-1)/2);
    }

    public static void main(String[] args) {
        int[] data = new int[]{8,6,9,2,5,1,7,10,3,4};
        HeapSort hs = new HeapSort(data);
        hs.sort();
        System.out.println(Arrays.toString(data));
    }
}

建堆两种方法：（两种方式产生的堆不一定一样，但根节点都是最大的）

可以从头到尾上浮一边，（上浮操作，保证了父节点不小于子节点）
也可以从最后一个非叶子节点开始到根节点做下沉操作。（下沉操作，保证了节点的左右子树均是堆）

将堆顶与最后元素交换后，因为左右子树都是堆，所以只要对堆顶做一次下沉操作即可。

------ 本文结束感谢您的阅读 ------

请我一杯咖啡吧！

微信打赏