12.trie树

trie树（字典树）

字典树，顾名思义，干嘛的？首先字典是干嘛的？查找字的。字典树自然也是起查找作用的，只不过是在树上找字的。为啥要在树上找字呢？因为我们都知道树上的操作更加高效。一般查找和更新操作的时间复杂度只与树的高度成正相关（貌似我们所有高效的数据结构都要往树上靠）。

我们先看一下几个问题：

1.我们输入n个单词，然后给出m个查询，每次查询一个单词，需要回答出这个单词是否在之前输入的n单词中出现过。

答：map计数（是STL中一种映射容器map<key,value>，这里key为单词，value为判断是否出现过的bool型标记），短小精悍。

2.我们输入n个单词，然后给出m个查询，每次查询一个单词的前缀，需要回答出 这个前缀 是之前输入的n单词中 多少个单词的前缀？

答：我们好像还是可以用map做，把输入n个单词中的每一个单词的前缀分别存入map中，然后计数，那这样真的很麻烦而且时间、空间复杂度会非常的高。若有n个单词，平均每个单词的长度为c，那么时间复杂度就会达到nc，很容易TLE。

在实际的搜索引擎中，当我们在数据库中搜索一个关键字的时候，如何快速准确的进行定位是一个关键的问题，在面临大规模数据的时候，使用暴力的手段往往会造成检索和查找性能的低下，因此我们需要更加高效的数据结构。

这时候我们引入一种新的数据结构：Trie树（字典树）。

原理

接下来我通过举个具体的例子让大家对字典树的原理有一个清晰的认识，我对cat、cash、apple、aply、ok建立一颗字典树，如下图所示：

从图中可以看出：

1.每一个节点代表一个字符

2.有相同前缀的单词在树中就有公共的前缀节点，由于一共有26个小写英文字母（在这篇文章中，我们主要讨论小写的英文字母查询），因此每个节点最多有26个子节点。

3.整棵树的根节点是空的（这里我们设置根节点为root=0），这便于查找和插入，可以通过根节点快速的进入树结构，稍后就会明白。

4.每个节点结束的时候用一个特殊的标记来表示，这里我们用-1来表示结束，从根节点到-1所经过的所有的节点对应一个英文单词。

基本操作

A. Insert，插入一个单词

如何插入？怎么用树结构去储存每一个单词呢，一个节点有26个子节点，每一个节点对应26字母中的一个字符，我们可以这样描述：编号为i的节点的第j个子节点是编号为k的节点。我们用数组tree[i][j]=k来表示。但是这里的i，k和j代表的意义是不一样的。i和k的编号是针对于整个树来说的，表示的位置编号，这个编号在树中可以唯一确定一个节点（位置+字符）。也就是说一个节点的字符和这个节点所在位置共同影响了这个点的编号，这个编号我们后续称之为绝对编号，相同的字符可能也会有不同的编号，因为位置可能不一样，如下面这种情况：

绝对编号，这个绝对编号字符按照插入的顺序编号，可以理解为一种dfs序

同一个字符a由于位置不同编号也不同。而j编号是相对于其父节点来说的，我们称之为相对编号，这个字符可能是父节点的第1个儿子a，可能是第2个儿子b，或者第26个儿子z，相当于有26个位置，针对不同的位置来对此字符施加编号，也就是如下图所示：

这个编号只取决于字符而与此字符所在位置无关。接下来我们用代码来实现一下这个插入字符的过程，比较简单，大家可以先自己写一下。

1
2
3
4
5
6
7
8
9
10

void Insert(char s[])
{
    int root=0;
    for(int i=0;s[i];i++)
    {
        int id=s[i]-'a';//相对编号
        if(tree[root][id]==-1) tree[root][id]=++cnt;//绝对编号
        root=tree[root][id];
    }
} 

我们一开始把tree数组都初始化为-1，往树中插入单词的时候，有单词的节点被非负数字覆盖，而-1则可以作为字符缺失的标志，也可以理解为此节点还没有被插入字符。

B. Search，查找

查找有很多种，可以查找一个前缀，也可以查找整个单词，也可以统计一个前缀在单词表中出现的次数。

我们这里以查找一个前缀是否出现过为例子进行讲解。

从左往右扫描前缀单词中的每一个字母，然后从字典树的第一层开始找，能找到第一个字母就顺着字典树往下走，否则结束查找，即没有此前缀；若前缀单词扫完了，表示有这个前缀。

代码如下 ：

1
2
3
4
5
6
7
8
9
10

int Search(char s[])
{
    int root=0;
    for(int i=0;s[i];i++)
    {
        int id=s[i]-'a';
        if(tree[root][id]==-1) return -1;
        root=tree[root][id];;
    }
}   

代码比较简单，但是我们进一步想统计前缀出现的次数怎么办？那就开一个sum[]数组，表示某节点被访问过的次数。我们知道对于每一个前缀单词的插入，只要出现过这个前缀，那么总是要遍历一次从根节点到这个前缀单词的终节点路径中所有的节点，在遍历每一个节点的时候，我们都让此节点的sum计数数组加一即可。而对于某个前缀出现的次数，我们最后只需要返回此前缀单词最后一个字符对应的sum值即可。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

void Insert(char s[])
{
    int root=0;
    for(int i=0;s[i];i++)
    {
        int id=s[i]-'a';
        if(tree[root][id]==0) tree[root][id]=++cnt;
        sum[tree[root][id]]++;
        root=tree[root][id];
    }
}
int Search(char s[])
{
    int root=0;
    for(int i=0;s[i];i++)
    {
        int id=s[i]-'a';
        if(tree[root][id]==0) return 0;
        root=tree[root][id];;
    }
    return sum[root];
}

只是 在之前的代码上增加了几行代码而已。好了整体来说，字典树就讲完了，更加复杂的操作在后续的专栏里会讲到。我们要掌握树的这种思想，如何高效地的储存数据，就比如这串代码里很关键的一个数组tree数组就可以很好的描述节点和节点之间的关系。在掌握思想之后，我们才能以不变应万变，用基本的思想去解决更加复杂的实际问题，事后呢我突然想写一个大规模数据的查询模块，觉得这个在实际中还是比较常用的，也可以去找一些更加高效算法来学习。

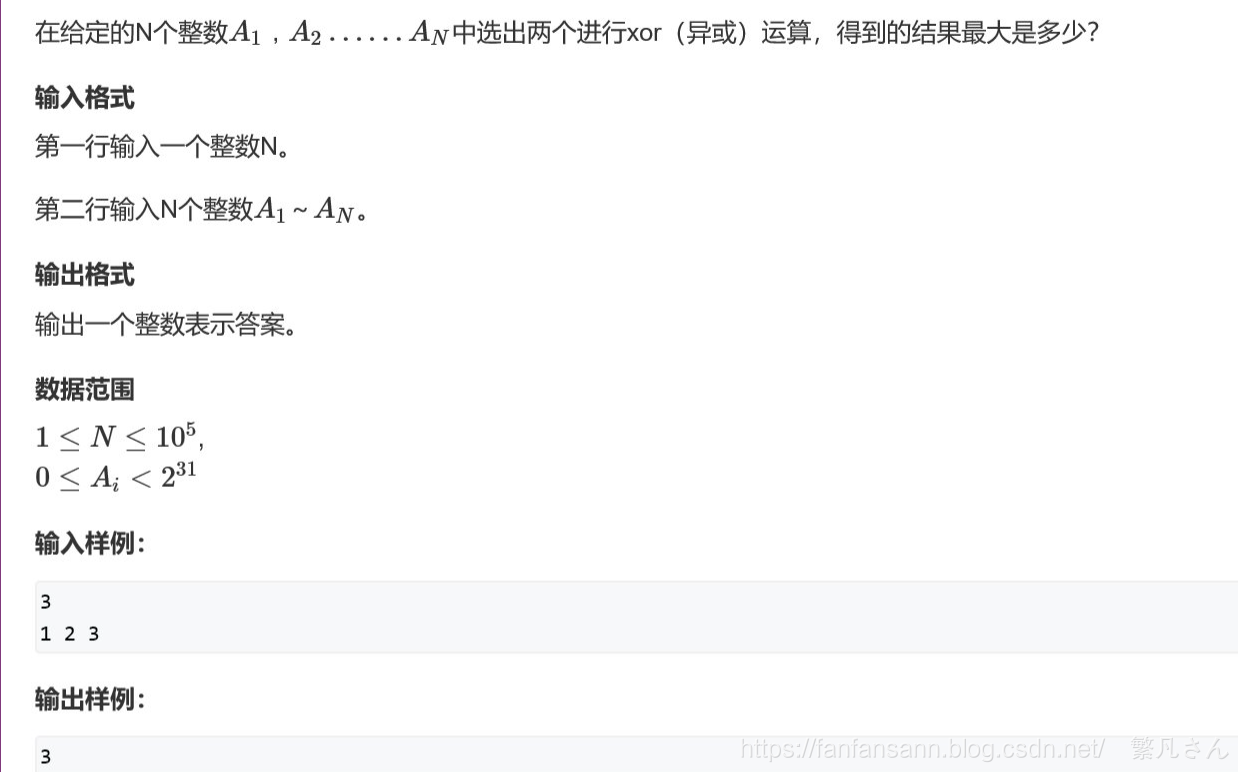
AcWing 143. 最大异或对

请我一杯咖啡吧！

赞赏

微信打赏