4.B树
前面讲的BST、AVL、红黑树都是典型的二叉查找树结构,其查找的时间复杂度与树高相关。那么降低树高自然对查找效率是有所帮助的。另外还有一个比较实际的问题:就是在大量数据存储中实现查询的场景下,平衡二叉树由于树深度过大而造成磁盘IO读写过于频繁,进而导致效率低下。那么如何减少树的深度(当然不能减少查询数据量),一个基本的想法就是:
①. 每个节点存储多个元素 (但元素数量不能无限多,否则查找就退化成了节点内部的线性查找了)。
②. 摒弃二叉树结构而采用多分支(多叉)树(由于节点内元素数量不能无限多,自然子树的数量也就不会无限多了)。
这样我们就提出了一个新的查找树结构 ——多路查找树。 根据AVL给我们的启发,一颗平衡多路查找树(B树)自然可以使得数据的查找效率保证在O(logN)这样的对数级别上。
1.B-树 (B树,平衡多路查找树)
可参考:《算法导论》第18章B树
注意,这里的B-Tree中的减号只是分隔符,我们通常在书或博客中见到的B-Tree或者B~Tree实际上指的都是B树。
B树是为磁盘或其他直接存储的辅助设备而设计的一种平衡搜索树。B树类似于红黑树,但它们在降低磁盘I/O操作次数方面要更好一些。许多数据库使用B树或B树的变种来存储信息。B树与红黑树不同之处在于B树的节点可以有多个孩子。B树类似于红黑树,就是含有n个节点的B树的高度为O(lgn)。
1.1B树的定义
一棵m阶的B-Tree有如下特性:
1. 每个节点最多有m个孩子。
2. 除了根节点和叶子节点外,其它每个节点至少有Ceil(m/2)个孩子。
3. 若根节点不是叶子节点,则至少有2个孩子
4. 所有叶子节点都在同一层,且不包含其它关键字信息
5. 每个非终端节点包含n个关键字信息(P0,P1,…Pn, k1,…kn)
6. 关键字的个数n满足:ceil(m/2)-1 <= n <= m-1
7. ki(i=1,…n)为关键字,且关键字升序排序。
8. Pi(i=1,…n)为指向子树根节点的指针。P(i-1)指向的子树的所有节点关键字均小于ki,但都大于k(i-1)
1.2B树的结构
B-Tree中的每个节点根据实际情况可以包含大量的关键字信息和分支,如下图所示为一个3阶的B-Tree:
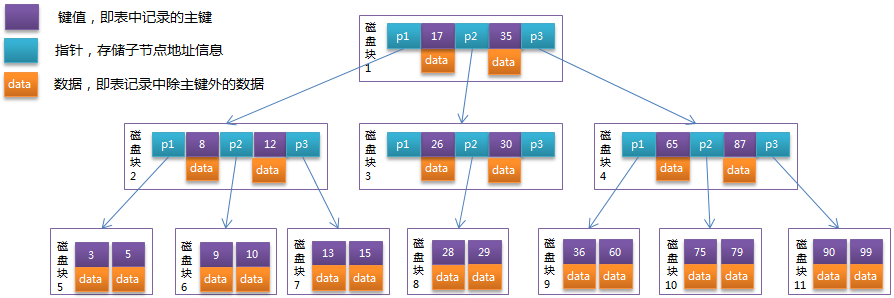
每个节点占用一个盘块的磁盘空间,一个节点上有两个升序排序的关键字和三个指向子树根节点的指针,指针存储的是子节点所在磁盘块的地址。两个关键词划分成的三个范围域对应三个指针指向的子树的数据的范围域。以根节点为例,关键字为17和35,P1指针指向的子树的数据范围为小于17,P2指针指向的子树的数据范围为17~35,P3指针指向的子树的数据范围为大于35。
1.3B树的查找过程
查找关键字29的过程:
- 根据根节点找到磁盘块1,读入内存。【磁盘I/O操作第1次】
- 比较关键字29在区间(17,35),找到磁盘块1的指针P2。
- 根据P2指针找到磁盘块3,读入内存。【磁盘I/O操作第2次】
- 比较关键字29在区间(26,30),找到磁盘块3的指针P2。
- 根据P2指针找到磁盘块8,读入内存。【磁盘I/O操作第3次】
- 在磁盘块8中的关键字列表中找到关键字29。
由于节点内部的关键字是有序的,所以在节点内部的查找可以使用二分法进行。
分析上面过程,发现需要3次磁盘I/O操作,和3次内存查找操作。由于内存中的关键字是一个有序表结构,可以利用二分法查找提高效率。而3次磁盘I/O操作是影响整个B-Tree查找效率的决定因素。B-Tree相对于AVLTree缩减了节点个数,使每次磁盘I/O取到内存的数据都发挥了作用,从而提高了查询效率。
 微信打赏
微信打赏